Answer:
The heat flow from the composite wall is 1283.263 watts.
Step-by-step explanation:
The conductive heat flow through a material, measured in watts, is represented by the following expression:
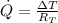
Where:
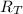 - Equivalent thermal resistance, measured in Celsius degrees per watt.
- Equivalent thermal resistance, measured in Celsius degrees per watt.
 - Temperature gradient, measured in Celsius degress.
- Temperature gradient, measured in Celsius degress.
First, the equivalent thermal resistance needs to be determined after considering the characteristics described below:
1) B and C are configurated in parallel and in series with A and D. (Section II)
2) A and D are configurated in series. (Sections I and III)
Section II

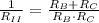
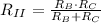
Section I
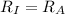
Section III
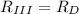
The equivalent thermal resistance is:
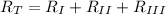
The thermal of each component is modelled by this:
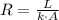
Where:
 - Thickness of the brick, measured in meters.
- Thickness of the brick, measured in meters.
 - Cross-section area, measured in square meters.
- Cross-section area, measured in square meters.
 - Thermal conductivity, measured in watts per meter-Celsius degree.
- Thermal conductivity, measured in watts per meter-Celsius degree.
If
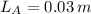 ,
,
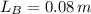 ,
,
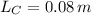 ,
,
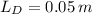 ,
,
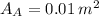 ,
,
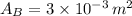 ,
,
 ,
,
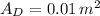 ,
,
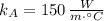 ,
,
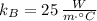 ,
,
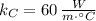 and
and
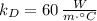 , then:
, then:
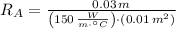
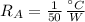
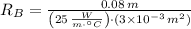
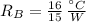
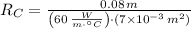
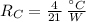
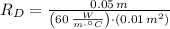
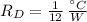
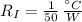

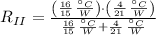
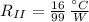
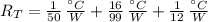
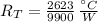
Now, if
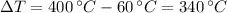 and
and
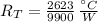 , the heat flow is:
, the heat flow is:
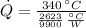
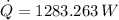
The heat flow from the composite wall is 1283.263 watts.