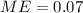Question

A new fertilizer was applied to the soil of 146 bean plants. 23% showed increased growth. Find the margin of error and 95% confidence interval for the percentage of all bean plants which show increased growth after application of the fertilizer. Round all answers to 2 decimal places.

Answer 1

The significance level for this case would be
`\alpha=1-0.95=0.05` and the critical value for this case would be:

`z_(\alpha/2)=1.96`

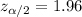
The margin of error is given by:

`ME = z_(\alpha/2) \sqrt{(\hat p (1-\hat p))/(n)}`

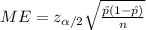
And replacing we got:

`ME = 1.96 \sqrt{(0.23*(1-0.23))/(146)} =0.0683`

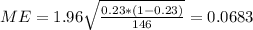
And the margin of error for this case would be
`ME = 0.07`

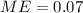
Explanation:

For this case we have the following dataset given:

`n= 146` represent the sample size

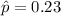`\hat p =0.23` represent the estimated proportion of interest

`Conf=0.95` represent the confidence level

The significance level for this case would be
`\alpha=1-0.95=0.05` and the critical value for this case would be:

`z_(\alpha/2)=1.96`

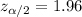
The margin of error is given by:

`ME = z_(\alpha/2) \sqrt{(\hat p (1-\hat p))/(n)}`

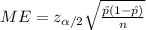
And replacing we got:

`ME = 1.96 \sqrt{(0.23*(1-0.23))/(146)} =0.0683`

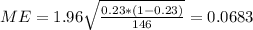
And the margin of error for this case would be
`ME = 0.07`