Answer:
The range of middle 98% of most averages for the lengths of pregnancies in the sample is, (261, 273).
Explanation:
The complete question is:
The lengths of pregnancies in a small rural village are normally distributed with a mean of 267 days and a standard deviation of 17 days. If you were to draw samples of size 47 from this population, in what range would you expect to find the middle 98% of most averages for the lengths of pregnancies in the sample?
Solution:
As the sample size is large, i.e. n = 47 > 30, the central limit theorem can be used to approximate the sampling distribution of sample mean by the normal distribution.
So,
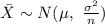
The range of the middle 98% of most averages for the lengths of pregnancies in the sample is the 98% confidence interval.
The critical value of z for 98% confidence level is,
z = 2.33
Compute the 98% confidence interval as follows:
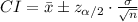

Thus, the range of middle 98% of most averages for the lengths of pregnancies in the sample is, (261, 273).