Question

The sound intensity level of a horn is 80dB. What is the sound intensity? The threshold of sound is 1x10-12W/m2.

Answer 1

The sound intensity is 1 x 10⁻⁴ W/m²

Step-by-step explanation:

Given;

sound intensity level, β = 80 dB

The threshold of sound or threshold intensity of hearing, I₀ = 1 x 10⁻¹² W/m²

Sound intensity level is given as;

`\beta = 10 Log((I)/(I_0) )`

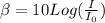
where;

β is the intensity level (dB)

I₀ is threshold intensity of hearing (W/m²)

I is the sound intensity (W/m²)

`\beta = 10Log((I)/(I_0)) \\\\(\beta)/(10) = Log((I)/(I_0))\\\\(80)/(10) = Log((I)/(I_0))\\\\8 = Log((I)/(I_0))\\\\10^(8) = (I)/(I_0)\\\\I = 10^(8) * I_0\\\\I = 10^(8) * 10^(-12) \ (W/m^2)\\\\I = 1*10^(-4) \ (W/m^2)`

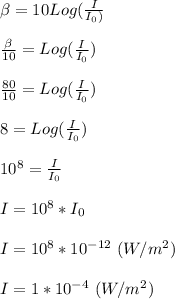
Therefore, the sound intensity is 1 x 10⁻⁴ W/m²

Answer 2

1.0x10^-4 W/m^2 as sound intensity

Step-by-step explanation:

Using

dB= 10log( I/Io)

Where Io= 10^-12W/m²

So dB=80dB

80= 10log(I/10^-12)

So

80/10= log (I/10^-12)

8= log (I/10^-12)

Taking the definition of log

10^8 = I/10^-12

I= 10^8 x10^ -12

I= 10^-4W/m² as sound intensity