Answer:
39896 miles will be traveled by at least 80% of the trucks
Explanation:
Given that :
the mean
 = 50000
= 50000
standard deviation
 = 12000
= 12000
we are to calculate how many miles will be traveled by at least 80% of the trucks.
This implies that :
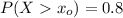
Likewise;
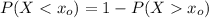
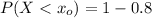
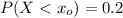
We all know that
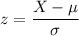
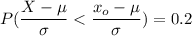
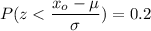
Using the z table to determine the value for (invNorm (0.2)); we have ;
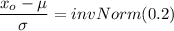
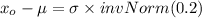

From z tables;
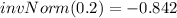

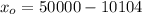
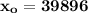
Thus; 39896 miles will be traveled by at least 80% of the trucks