Question

ABC trucking company realized that on an annual basis that distance traveled is normally distrubuted with a mean of 50,000 miles and a standard deviation of 12,000 HOw many miles will be traveled by at least 80% of the trucks

Answer 1

39896 miles will be traveled by at least 80% of the trucks

Explanation:

Given that :

the mean
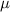`\mu` = 50000

standard deviation
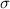`\sigma` = 12000

we are to calculate how many miles will be traveled by at least 80% of the trucks.

This implies that :

`P(X > x_o) = 0.8`

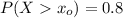
Likewise;

`P(X < x_o) = 1- P(X > x_o)`

`P(X < x_o) = 1-0.8`

`P(X < x_o) = 0.2`

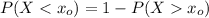
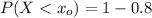
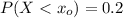
We all know that

`z = (X- \mu)/(\sigma)`

`P((X- \mu)/(\sigma)< (x_o - \mu )/(\sigma)) = 0.2`

`P({z < (x_o - \mu )/(\sigma)) = 0.2`

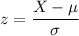
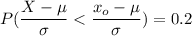
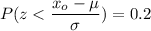
Using the z table to determine the value for (invNorm (0.2)); we have ;

`(x_o - \mu )/(\sigma) = invNorm (0.2)`

`{x_o - \mu } = {\sigma} * invNorm (0.2)`

`{x_o } = \mu + {\sigma} * invNorm (0.2)`

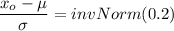
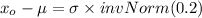
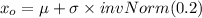
From z tables;
`invNorm (0.2)= -0.842`

`{x_o } = 50000 + 12000 *(-0.842)`

`{x_o } = 50000 -10104`

`\mathbf{{x_o } =39896}`

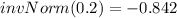
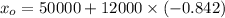
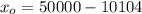
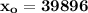
Thus; 39896 miles will be traveled by at least 80% of the trucks