Question

Outside temperature over a day can be modelled as a sinusoidal function. Suppose you know the high temperature for the day is 100 degrees and the low temperature of 70 degrees occurs at 5 AM. Assuming t is the number of hours since midnight, find an equation for the temperature, D, in terms of t. Assume the next low is 24 hours later.

Answer 1

The function for the outside temperature is represented by
`T(t) = 85\º + 15\º \cdot \sin \left[(t-6\,h)/(24\,h) \right]`, where t is measured in hours.

Explanation:

Since outside temperature can be modelled as a sinusoidal function, the period is of 24 hours and amplitude of temperature and average temperature are, respectively:

Amplitude

`A = (100\º-70\º)/(2)`

`A = 15\º`

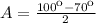
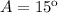
Mean temperature

`\bar T = (70\º+100\º)/(2)`

`\bar T = 85\º`

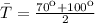
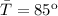
Given that average temperature occurs six hours after the lowest temperature is registered. The temperature function is expressed as:

`T(t) = \bar T + A \cdot \sin \left[2\pi\cdot(t-6\,h)/(\tau) \right]`

Where:

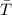`\bar T` - Mean temperature, measured in degrees.

`A` - Amplitude, measured in degrees.

`\tau` - Daily period, measured in hours.

`t` - Time, measured in hours. (where t = 0 corresponds with 5 AM).

If
`\bar T = 85\º`,
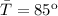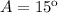`A = 15\º` and
`\tau = 24\,h`, the resulting function for the outside temperature is:

`T(t) = 85\º + 15\º \cdot \sin \left[(t-6\,h)/(24\,h) \right]`