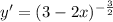Question

Find dy/dx of (3 - 2x)-1/2

Answer 1

Explanation:

To evaluate the derivative of this function you need the chain rule. The pattern I teach to my calculus students is to find

u =

u' =

f(u) =

f'(u) =

First pick your "u". u will be the inner function, the one inside the parenthesis.

u' will then be the derivative of u.

f(u) is the function in terms of u, and

f'(u) is the derivative of the function in terms of u.

The derivative then, finally, will be u' * f'(u). Let's begin.

Our u, or the part of the function inside the parenthesis is 3 - 2x; hence,

u = 3 - 2x

The derivative, u', then is

u' = -2

f(u) is the function in terms of u, so

f(u) =
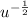`u^{-(1)/(2)` and the derivative in terms of u is

f'(u) =
`-(1)/(2)u^{-(3)/(2)`

u' * f'(u) then is

`-(1)/(2)u^{-(3)/(2)*(-2)` Simplify that by subbing back in for u and multiplying -2 by -1/2 to get

`y'=(3-2x)^{-(3)/(2)`