Answer:
4x + 6
Step-by-step explanation:

To determine what the numerator would be, after simplifying both fractions, take the following steps:
Step 1: Factorise the denominator of the first fraction, x² + 3x + 2.
Thus,
x² + 2x + x + 2
(x² + 2x) + (x + 2)
x(x + 2) +1(x + 2)
(x + 1)(x + 2)
We would now have the following as our new fractions to add together and simplify:
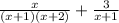
Step 2: find the highest common factor of the denominator of both fractions.
Highest common factor of (x + 1)(x + 2) and (x + 1) = (x + 1)(x + 2)
Step 3: To add both fractions, divide the highest common factor gotten in step 2 by each denominator, and then multiply the result by the numerator of each fraction.
Thus,
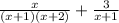
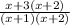
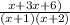
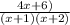
Therefore, the numerator of the simplified form sum of both fractions = 4x + 6