Answer:
The specific volume is reduced in 80 per cent due to isothermal compression.
Specific enthalpy remains constant.
Step-by-step explanation:
Let suppose that neon behaves ideally, the equation of state for ideal gases is:
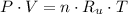
Where:
 - Pressure, measured in kilopascals.
- Pressure, measured in kilopascals.
 - Volume, measured in cubic meters.
- Volume, measured in cubic meters.
 - Molar quantity, measured in kilomoles,
- Molar quantity, measured in kilomoles,
 - Temperature, measured in kelvins.
- Temperature, measured in kelvins.
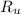 - Ideal gas constant, measured in
- Ideal gas constant, measured in
 .
.
On the other hand, the molar quantity (
 ) and specific volume (
) and specific volume (
 ), measured in cubic meter per kilogram, are defined as:
), measured in cubic meter per kilogram, are defined as:
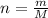 and
and
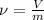
Where:
 - Mass of neon, measured in kilograms.
- Mass of neon, measured in kilograms.
 - Molar mass of neon, measured in kilograms per kilomoles.
- Molar mass of neon, measured in kilograms per kilomoles.
After replacing in the equation of state, the resulting expression is therefore simplified in term of specific volume:
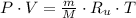

Since the neon is compressed isothermally, the following relation is constructed herein:
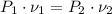
Where:
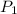 ,
,
 - Initial and final pressure, measured in kilopascals.
- Initial and final pressure, measured in kilopascals.
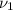 ,
,
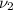 - Initial and final specific volume, measured in cubic meters per kilogram.
- Initial and final specific volume, measured in cubic meters per kilogram.
The change in specific volume is given by the following expression:
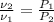
Given that
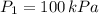 and
and
 , the change in specific volume is:
, the change in specific volume is:
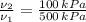
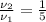
The specific volume is reduced in 80 per cent due to isothermal compression.
Under the ideal gas supposition, specific enthalpy is only function of temperature, as neon experiments an isothermal process, temperature remains constant and, hence, there is no change in specific enthalpy.
Specific enthalpy remains constant.