Question

g The "Coulomb barrier" is defined to be the electric potential energy of a system of two nuclei when their surfaces barely touch. The probability of a nuclear reaction greatly increases if the energy of the system is above this barrier. What is the Coloumb barrier (in MeV) for the absorption of an alpha particle by a lead-208 nucleus

Answer 1

The Coulomb Barrier U is 25.91 MeV

Step-by-step explanation:

Given that:

Atomic Mass of lead nucleus A = 208

atomic mass of an alpha particle A = 4

Radius of an alpha particle
`R_\alpha = R_o A^{^{(1)/(3)}`

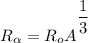
where;

`R_\alpha = 1.2 * 10 ^(-15) \ m`

`R_\alpha = R_o A^{^{(1)/(3)}`

`R_\alpha = 1.2 * 10 ^(-15) \ m * (4) ^{^{(1)/(3)}`

`R_\alpha = 1.905 * 10^(-15) \ m`

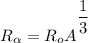
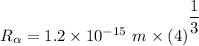
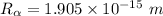
Radius of the Gold nucleus

`R_(Au)= R_o A^{^{(1)/(3)}`

`R_(Au)= 1.2 * 10 ^(-15) \ m * (208) ^{^{(1)/(3)}`

`R_(Au) = 7.11 * 10^(-15) \ m`

`R = R_\alpha + R_(Au)`

`R = 1.905 * 10^(-15) \ m + 7.11 * 10^(-15) \ m`

`R = 9.105 * 10 ^(-15) \ m`

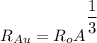
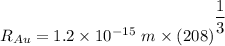
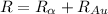
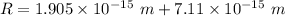
The electric potential energy of the Coulomb barrier
`U = (Ke \ q_(\alpha) q_(Au))/(R)`

`U = \frac{8.99 * 10^9 \ N.m \ ^2/C ^2 \ * 2 ( 82) * \(1.60 * 10^(-19) C \ \ e } {9.105 * 10^(-15) \ m }`

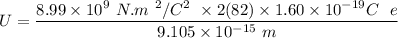
U = 25908577.7eV

U = 25.908577 × 10⁶ eV

U = 25.91 MeV

The Coulomb Barrier U is 25.91 MeV