Answer:
The Coulomb Barrier U is 25.91 MeV
Step-by-step explanation:
Given that:
Atomic Mass of lead nucleus A = 208
atomic mass of an alpha particle A = 4
Radius of an alpha particle
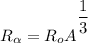
where;
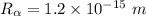
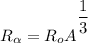
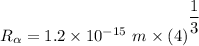
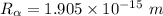
Radius of the Gold nucleus
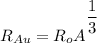
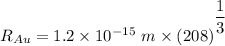
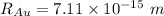
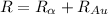
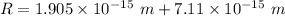
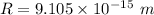
The electric potential energy of the Coulomb barrier
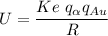
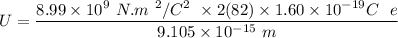
U = 25908577.7eV
U = 25.908577 × 10⁶ eV
U = 25.91 MeV
The Coulomb Barrier U is 25.91 MeV