Question

On a coordinate plane, 2 exponential fuctions are shown. Function f (x) decreases from quadrant 2 into quadrant 1 and approaches y = 0. It crosses the y-axis at (0, 6) and goes through (1, 2). Function g (x) approaches y = 0 in quadrant 2 and increases into quadrant 1. It goes through (negative 1, 2) and crosses the y-axis at (0, 6).

Which function represents g(x), a reflection of f(x) = 6(one-third) Superscript x across the y-axis?



g(x) = −6(one-third) Superscript x


g(x) = −6(one-third) Superscript negative x


g(x) = 6(3)x


g(x) = 6(3)−x

Answer 1

C) g(x) = 6(3)x

Answer 2

`g(x)=6(3)^x`

Explanation:

We are given that

`f(x)=6((1)/(3))^x`

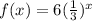
Function f decreases from quadrant 2 to quadrant 1 and approaches y=0

It cut the y- axis at (0,6) and passing through the point (1,2).

Function g(x) approaches y=0 in quadrant 2 and increases into quadrant 1.

It passing through the point (-1,2) and cut the y-axis at point (0,6).

Reflection across y- axis:

Rule of transformation is given by

`(x,y)\rightarrow (-x,y)`

Using the rule then we get

`g(x)=6((1)/(3))^(-x)=6(3)^x`

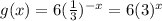
By using

`x^(-a)=(1)/(x^a)`

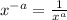
Substitute x=-1

`g(-1)=6* ((1)/(3))=2`

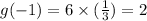
Substitute x=0

`g(0)=6`

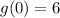
Therefore,
`g(x)=6(3)^x` is true.