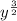2 Answers

Kevin Carmody · Answer 1 · 2021-10-08T09:09:38+0000

Answer:

$y^{ (3)/(2)}$

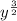
Explanation:

From the question posted, you've already initiated the solution but you applied a wrong approach;

Given

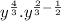
$y^{(4)/(3)} . y^{(2)/(3) - (1)/(2)}$

Required

Simplify; using power property

Power property states that;

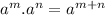
a^m.a^n = a^(m+n)

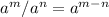
a^m/a^n = a^(m-n)

By comparison; we have to apply the first property;

This is shown below;

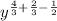
$y^{(4)/(3)+(2)/(3) - (1)/(2)}$

Add fraction of the same numerator

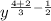
$y^{(4+2)/(3) - (1)/(2)}$

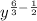
$y^{(6)/(3) - (1)/(2)}$

$y^{2 - (1)/(2)}$

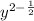
Subtract fraction

$y^{ (4-1)/(2)}$

$y^{ (3)/(2)}$

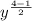
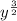
The expression
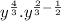$y^{(4)/(3)} . y^{(2)/(3) - (1)/(2)}$ is equivalent to
$y^{ (3)/(2)}$

Please log in or register to add a comment.