Question

g Determine the area of the region between the two curves by integrating over the x-axis. y = x2 − 24 and y = 1

Answer 1

A = 166.66

Explanation:

You have the following functions:

`y_1=x^2-24\\\\y_2=1`

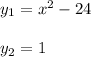
In order to calculate the area of the given region, you first calculate the points at which the function y = x^2-24 intersects the line y=1:

`1=x^2-24\\\\0=x^2-25\\\\x=√(25)=\pm 5`

Next, you take into account that the area between the two function is given by:

Where you have used the fact that y2 is above the y1 function.

Next, you calculate the following integral:

`A=\int_(-5)^(5)(1-(x^2-24))dx=\int_(-5)^(5)(25-x^2)dx\\\\A=(25x-(1)/(3)x^3)|_(-5)^(5)\\\\A=(25(5)-(1)/(3)(125))-(25(-5)-(1)/(3)(-125))\\\\A=166.66`

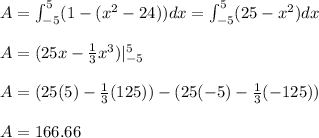
Then, the area of the bounded region is 166.66