Answer:
The answer to this question can be defined as follows:
Step-by-step explanation:
The risk-free rate of T-bill is (r f), which is 4.4% = 0.044. The fund for stocks (S) An expected 14% = 0.14 return and the value of the standard deviation is 34% = 0.34. The Announcement fund of (B) and the estimated 5% = 0.05 return, with a standard deviation 28% = 0.28 .
following are the formula for the equation is:
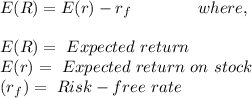
Using the formula to measure the projected return for bond and stock fund:
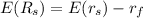
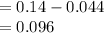
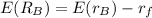
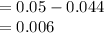
Measure mass with optimized risk for stock index fund (S) and Bond Fund (B), Introduce to investment as follows:
![W_s=(E(R_s)\sigma_(B)^2-E(R_B) Cov(r_s,r_s))/(E(R_s)\sigma_B^2+E(R_B)\sigma_s^2-[E(R_s)+E(R_s)]Cov(r_s,r_s))](https://img.qammunity.org/2021/formulas/business/college/5e3et91iqir1jzizyat03tpyszozn4xlvo.png)
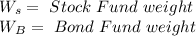
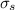
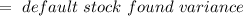

Measure the portfolio and bond fund covariance according to:
Bond and equity fund covariance
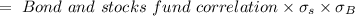
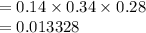
Measure the mass of the stock and bond fund as follows:
![W_s=(E(R_s)\sigma_(B)^2-E(R_B) Cov(r_s,r_s))/(E(R_s)\sigma_B^2+E(R_B)\sigma_s^2-[E(R_s)+E(R_s)]Cov(r_s,r_s))](https://img.qammunity.org/2021/formulas/business/college/5e3et91iqir1jzizyat03tpyszozn4xlvo.png)
![=(0.096 * 0.28^2-0.006* 0.013328)/(0.096 * 0.28^2+0.006* 0.34^2-[0.096+0.006]* 0.013328)](https://img.qammunity.org/2021/formulas/business/college/byyfr91amssd3m127fe1jd7uuk70yi80ae.png)

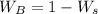
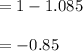
The correspondence(p) here is 0.14. Calculate the norm for the maximum risky as follows:
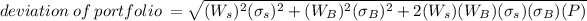
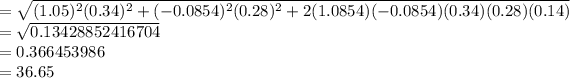
The standard deviation for the optimal risky portfolio is 36.65%
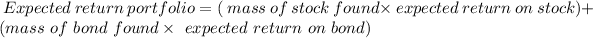
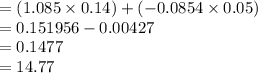
The optimal risk portfolio is 14.77%