Question

A pension fund manager is considering three mutual funds. The first is a stock fund, the second is a long-term government and corporate bond fund, and the third is a T-bill money market fund that yields a rate of 4.4%. The probability distribution of the risky funds is as follows:

Expected Return Standard Deviation
Stock fund (S) 14% 34%
Bond fund (B) 5 28
The correlation between the fund returns is 0.14.
Solve numerically for the proportions of each asset and for the expected return and standard deviation of the optimal risky portfolio. (Do not round intermediate calculations and round your final answers to 2 decimal places. Omit the "%" sign in your response.)
Portfolio invested in the stock %
Portfolio invested in the bond %
Expected return %
Standard deviation %

Answer 1

The answer to this question can be defined as follows:

Step-by-step explanation:

The risk-free rate of T-bill is (r f), which is 4.4% = 0.044. The fund for stocks (S) An expected 14% = 0.14 return and the value of the standard deviation is 34% = 0.34. The Announcement fund of (B) and the estimated 5% = 0.05 return, with a standard deviation 28% = 0.28 .

following are the formula for the equation is:

`E(R)=E(r)-r_f \ \ \ \ \ \ \ \ \ \ \ \ where, \\\\E(R)= \ Expected \ return\\E (r) = \ Expected \ return \ on \ stock \\(r_f)= \ Risk-free \ rate`

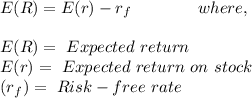
Using the formula to measure the projected return for bond and stock fund:

`E(R_s)=E(r_s)-r_f\\`

`=0.14-0.044\\ =0.096\\`

`E(R_B)=E(r_B)-r_f`

`= 0.05-0.044\\= 0.006`

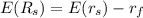
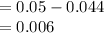
Measure mass with optimized risk for stock index fund (S) and Bond Fund (B), Introduce to investment as follows:

`W_s=(E(R_s)\sigma_(B)^2-E(R_B) Cov(r_s,r_s))/(E(R_s)\sigma_B^2+E(R_B)\sigma_s^2-[E(R_s)+E(R_s)]Cov(r_s,r_s))`

`W_s = \ Stock \ Fund \ weight \\ W_B = \ Bond \ Fund \ weight \\`

`\sigma_s`
`= \ de fault \ stock \ found \ variance\\`

`\sigma_(B)= \ Bond \ Fund \ standard \ deviation \\r_s = \ Stock \ fund \ planned \ return \\r_B = \ Bond \ fund's \ projected \ return\\ Cov(r_s, r_B)= \ Pension \ and \ bond \ fund \ covariance\\`

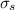
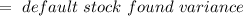
Measure the portfolio and bond fund covariance according to:

Bond and equity fund covariance
`= \ Bond \ and \ stocks \ fund \ correlation * \sigma_s * \sigma_B`

`= 0.14 * 0.34 * 0.28\\= 0.013328\\`

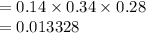
Measure the mass of the stock and bond fund as follows:

`W_s=(E(R_s)\sigma_(B)^2-E(R_B) Cov(r_s,r_s))/(E(R_s)\sigma_B^2+E(R_B)\sigma_s^2-[E(R_s)+E(R_s)]Cov(r_s,r_s))`

`=(0.096 * 0.28^2-0.006* 0.013328)/(0.096 * 0.28^2+0.006* 0.34^2-[0.096+0.006]* 0.013328)`

`=(0.0075264-0.000079968)/(0.0075264+0.0006936-0.001359456)\\\\=(0.007446432)/(0.006860544)\\\\=1.085\\`

`W_B=1-W_s\\\\`

`=1-1.085\\\\=-0.85`

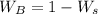
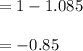
The correspondence(p) here is 0.14. Calculate the norm for the maximum risky as follows:

`\ deviation \ of \ portfolio \ =√((W_s)^2 (\sigma_s)^2+(W_B)^2 (\sigma_B)^2+ 2(W_s)(W_B)(\sigma_s) (\sigma_B) (P))`

`=√((1.05)^2 (0.34)^2+(-0.0854)^2 (0.28)^2+ 2(1.0854)(-0.0854)(0.34) (0.28) (0.14))\\=√(0.13428852416704)\\=0.366453986\\=36.65%`

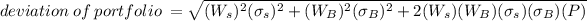
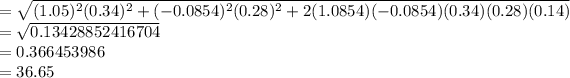
The standard deviation for the optimal risky portfolio is 36.65%

`\ Expected \ return \ portfolio = (\ mass \ of \ stock \ found * \ expected \ return \ on\ stock)+ ( mass \ of \ bond\ found * \ expected \ return \ on\ bond)`
`=(1.085* 0.14)+(-0.0854 * 0.05)\\= 0.151956-0.00427\\=0.1477\\=14.77%\\`

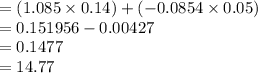
The optimal risk portfolio is 14.77%