Question

The Demon family owns a large grape vineyard in western New York along Lake Erie. The grapevines must be sprayed at the beginning of the growing season to protect against various insects. Two new insecticides have just been marketed: Pernod 5 and Action. To test their effectiveness, three long rows were selected and sprayed with Pernod 5, and three other were sprayed with Action. When the grape ripened, 400 of the vines treated with Pernod 5 and 400 of the vines treated with Action were checked for infestation. The number of infested vines treated with Pernod 5 and Action are 24 and 40 respectively.

At 0.05 significance level, can we conclude that there is a difference in the proportion of vines infested using Pernod 5 as opposed to Action?​

Answer 1

At a significance level of 0.05, there is enough evidence to support the claim that there is a significant difference in the proportion of vines infested using Pernod 5 as opposed to Action.

Explanation:

This is a hypothesis test for the difference between proportions.

The claim is that there is a significant difference in the proportion of vines infested using Pernod 5 as opposed to Action.

Then, the null and alternative hypothesis are:

H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2\\eq 0

The significance level is 0.05.

The sample 1 (Pernod 5), of size n1=400 has a proportion of p1=0.06.

`p_1=X_1/n_1=24/400=0.06`

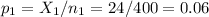
The sample 2, of size n2=400 has a proportion of p2=0.1.

`p_2=X_2/n_2=40/400=0.1`

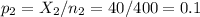
The difference between proportions is (p1-p2)=-0.04.

`p_d=p_1-p_2=0.06-0.1=-0.04`

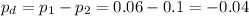
The pooled proportion, needed to calculate the standard error, is:

`p=(X_1+X_2)/(n_1+n_2)=(24+40)/(400+400)=(64)/(800)=0.08`

The estimated standard error of the difference between means is computed using the formula:

`s_(p1-p2)=\sqrt{(p(1-p))/(n_1)+(p(1-p))/(n_2)}=\sqrt{(0.08*0.92)/(400)+(0.08*0.92)/(400)}\\\\\\s_(p1-p2)=√(0.000184+0.000184)=√(0.000368)=0.019`

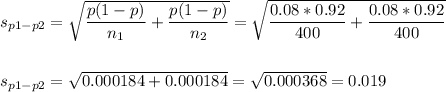
Then, we can calculate the z-statistic as:

`z=(p_d-(\pi_1-\pi_2))/(s_(p1-p2))=(-0.04-0)/(0.019)=(-0.04)/(0.019)=-2.085`

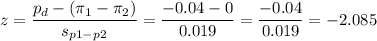
This test is a two-tailed test, so the P-value for this test is calculated as (using a z-table):

`\text{P-value}=2\cdot P(z<-2.085)=0.037`

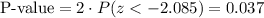
As the P-value (0.037) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that there is a significant difference in the proportion of vines infested using Pernod 5 as opposed to Action.