Answer:
(a)
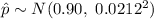
(b)
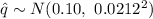
(c) Not different.
Explanation:
The information provided is:
- The age at first startup for 90% of entrepreneurs was 29 years of age or less.
- The age at first startup for 10% of entrepreneurs was 30 years of age or more.
According to the Central limit theorem, if from an unknown population large samples of sizes n > 30, are selected and the sample proportion for each sample is computed then the sampling distribution of sample proportion follows a Normal distribution.
The mean of this sampling distribution of sample proportion is:
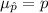
The standard deviation of this sampling distribution of sample proportion is:
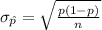
(a)
Let p represent the proportion of entrepreneurs whose first startup was at 29 years of age or less.
A sample of n = 200 entrepreneurs is selected.
As n = 200 > 30, according to the Central limit theorem the sampling distribution of sample proportion can be approximated by the normal distribution.
Compute the mean and standard deviation as follows:
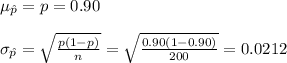
So,
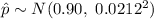 .
.
(b)
Let q represent the proportion of entrepreneurs whose first startup was at 30 years of age or more.
A sample of n = 200 entrepreneurs is selected.
As n = 200 > 30, according to the Central limit theorem the sampling distribution of sample proportion can be approximated by the normal distribution.
Compute the mean and standard deviation as follows:
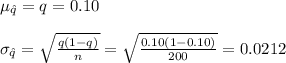
So,
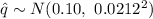 .
.
(c)
The standard deviation of sample proportions is also known as the standard error.
The standard deviation of p is, 0.0212.
The standard deviation of q is, 0.0212.
Thus, the standard errors of the sampling distributions in parts (a) and (b) are same.