Question

SPEAR is a storage ring at the Stanford Linear Accelerator which has a circulating beam of electrons that are moving at nearly the speed of light (2.998 108 m/s). If a similar ring is about 80.0 m in diameter and has a 0.59 A beam, how many electrons are in the beam

Answer 1

n = 3.1x10¹²

Step-by-step explanation:

To find the number of electrons we need to find first the charge (q):

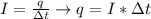`I = (q)/(\Delta t) \rightarrow q = I*\Delta t` (1)

Where:

I: is the electric current = 0.59 A

t: is the time

The time t is equal to:

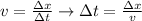`v = (\Delta x)/(\Delta t) \rightarrow \Delta t = (\Delta x)/(v)` (2)

Where:

x: is the displacement

v: is the average speed = 2.998x10⁸ m/s

The displacement is equal to the perimeter of the circumference:

`\Delta x = 2\pi*r = \pi*d` (3)

Where d is the diameter = 80.0 m

By entering equations (2) and (3) into (1) we have:

`q = I*\Delta t = I*(\Delta x)/(v) = (I\pi d)/(v) = (0.59 A*\pi*80.0 m)/(2.99 \cdot 10^(8) m/s) = 4.96 \cdot 10^(-7) C`

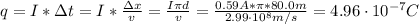
Now, the number of electrons (n) is given by:

`n = (q)/(e)`

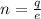
Where e is the electron's charge = 1.6x10⁻¹⁹ C

`n = (q)/(e) = (4.96 \cdot 10^(-7) C)/(1.6 \cdot 10^(-19) C) = 3.1 \cdot 10^(12)`

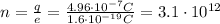
Therefore, the number of electrons in the beam is 3.1x10¹².

I hope it helps you!