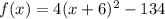Question

The first steps in writing f(x) = 4x2 + 48x + 10 in vertex form are shown. f(x) = 4(x2 + 12x) + 10 (twelve-halves) squared = 36 What is the function written in vertex form?

Answer 1

C

Explanation:

I just finished the unit test on Edge. and got a 100% and I selected "c" as my answer.

Answer 2

`f(x)=4(x+6)^2-134`

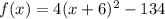
Explanation:

We are required to write the function
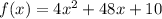`f(x) = 4x^2 + 48x + 10` in vertex form.

First, bring the constant to the left-hand side.

`f(x) -10= 4x^2 + 48x`

Factorize the right hand side.

`f(x) -10= 4(x^2 + 12x)`

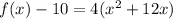
Take note of the factored term(4) and write it in the form below.

`f(x) -10+4\Box= 4(x^2 + 12x+\Box)`

`\Box = (\frac{\text{Coefficient of x}}{2} )^2\\\\\text{Coefficient of x}=12\\\\\Box = ((12)/(2) )^2 =6^2=36`

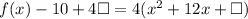
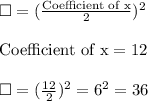
Substitute 36 for the boxes.

`f(x) -10+4\boxed{36}= 4(x^2 + 12x+\boxed{36})`

`f(x) -10+144= 4(x^2 + 12x+6^2)`

`f(x) +134= 4(x+6)^2\\f(x)=4(x+6)^2-134`

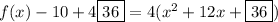
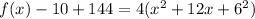
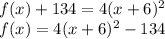
The function written in vertex form is
`f(x)=4(x+6)^2-134`