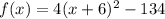Answer:
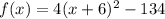
Explanation:
We are required to write the function
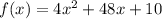 in vertex form.
in vertex form.
First, bring the constant to the left-hand side.
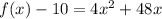
Factorize the right hand side.
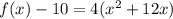
Take note of the factored term(4) and write it in the form below.
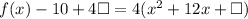
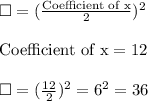
Substitute 36 for the boxes.
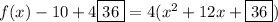
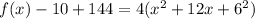
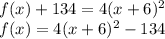
The function written in vertex form is