Answer:
The 98% confidence interval for the population mean number of hours worked per year per person is (2146, 2193).
Explanation:
The question is incomplete.
The number of hours registered in the sample are:
2051 2061 2162 2167 2169 2171
2180 2183 2186 2195 2196 2198
2205 2210 2211
The sample mean can be calculated as:

We have to calculate a 98% confidence interval for the mean.
The population standard deviation is know and is σ=39.
The sample mean is M=2169.67.
The sample size is N=15.
As σ is known, the standard error of the mean (σM) is calculated as:
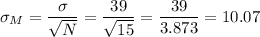
The z-value for a 98% confidence interval is z=2.326.
The margin of error (MOE) can be calculated as:

Then, the lower and upper bounds of the confidence interval are:
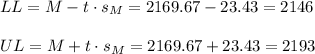
The 98% confidence interval for the population mean is (2146, 2193).