Question

The number of hours worked per year per person in a state is normally distributed with a standard deviation of 39. A sample of 15 people is selected at random, and the number of hours worked per year per person is given below. Calculate the 98% confidence interval for the mean hours worked per year in this state. Round your answers to the nearest integer and use ascending order.

Answer 1

The 98% confidence interval for the population mean number of hours worked per year per person is (2146, 2193).

Explanation:

The question is incomplete.

The number of hours registered in the sample are:

2051 2061 2162 2167 2169 2171

2180 2183 2186 2195 2196 2198

2205 2210 2211

The sample mean can be calculated as:

`M=(1)/(n)\sum_(i=1)^n\,x_i\\\\\\M=(1)/(15)(2051+2061+2162+2167+2169+2171+2180+2183+2186+2195+2196+2198+2205+2210+2211)\\\\\\M=(32545)/(15)\\\\\\M=2169.67\\\\\\`

We have to calculate a 98% confidence interval for the mean.

The population standard deviation is know and is σ=39.

The sample mean is M=2169.67.

The sample size is N=15.

As σ is known, the standard error of the mean (σM) is calculated as:

`\sigma_M=(\sigma)/(√(N))=(39)/(√(15))=(39)/(3.873)=10.07`

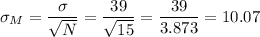
The z-value for a 98% confidence interval is z=2.326.

The margin of error (MOE) can be calculated as:

`MOE=z\cdot \sigma_M=2.326 \cdot 10.07=23.43`

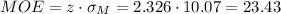
Then, the lower and upper bounds of the confidence interval are:

`LL=M-t \cdot s_M = 2169.67-23.43=2146\\\\UL=M+t \cdot s_M = 2169.67+23.43=2193`

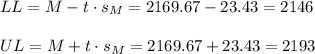
The 98% confidence interval for the population mean is (2146, 2193).