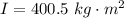Question

A 133 kg horizontal platform is a uniform disk of radius 1.95 m and can rotate about the vertical axis through its center. A 62.7 kg person stands on the platform at a distance of 1.19 m from the center, and a 28.5 kg dog sits on the platform near the person 1.45 m from the center. Find the moment of inertia of this system, consisting of the platform and its population, with respect to the axis.

Answer 1

The moment of inertia of the system is
`I = 400.5 \ kg \cdot m^2`

Step-by-step explanation:

From the question we are told that

The mass of the platform is
`m = 133\ kg`

The radius of the platform is r = 1.95 m

The mass of the person is
`m_p = 62.7 \ kg`

The position of the person from the center is
`d = 1.19 \ m`

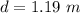
The mass of the dog is
`m_D = 28.5 \ kg`

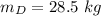
The position of the dog from the center is
`D = 1.45 \ m`

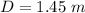
Generally the moment of inertia of the platform with respect to its axis is mathematically represented as

`I_p = (m r^2)/(2)`

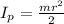
The moment of inertia of the person with respect to the axis is mathematically represented as

`I_z = m_p* d^2`

The moment of inertia of the dog with respect to the axis is mathematically represented as

`I_D = m_d * D^2`

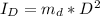
So the moment of inertia of the system about the axis is mathematically evaluated as

`I = I_p + I_z + I_D`

=>
`I = (mr^2)/(2) + m_p * d^2 + m_d * D^2`

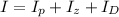
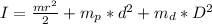
substituting values

`I = ((133) * (1.95)^2)/(2) + (62.7) * (1.19)^2 + (28.5) * (1.45)^2`

`I = 400.5 \ kg \cdot m^2`