Answer:
The correct options are;
To determine if it is a parallelogram use the converse of the parallelogram diagram diagonal theorem. This states that if the diagonals bisect each other, then the quadrilateral is a parallelogram
The midpoint of
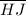 is (2, 2) and the midpoint of
is (2, 2) and the midpoint of
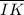 is (2, 2)
is (2, 2)
Therefore, HIJK is a parallelogram because the diagonals have the same (share a common) midpoint, which means they bisect each other
Explanation:
The given coordinates are;
H(0, 5), I(3, 3), J(4, -1), K(1, 1)
The diagonals are;
HJ and IK
The equations of the diagonals are;
Slope of segment HJ = (5 - (-1))/(0 - 4) = -3/2
Therefore, y - 5 = -3/2(x - 0)
When x = 0, y = 5, therefore c = 0 which gives;
y = -3/2x + 5
The slope of segment IK = (3 - 1)/(3 - 1) = 1
Therefore, y - 3 = x - 3
y = x
To get the intersection point, we have;
-3/2x + 5 = x
5 = 5/2x
x = 5/(5/2) = 2
y = x = 2
The coordinate of the intersection point is (2, 2)
The coordinates of the mid point if gotten from ((x₁ + x₂)/2, (y₁ + y₂)/2)
For HJ, we have;
((0 + 4)/2, (5 + (-1))/2) = (2, 2)
The coordinate of the midpoint of IK is ((3 + 1)2, (3 + 1)/2) = (2, 2)
Therefore, the diagonals bisect each other
Therefore we have;
To determine if it is a parallelogram use the converse of the parallelogram diagram diagonal theorem . This states that if the diagonals bisect each other, then the quadrilateral is a parallelogram
The midpoint of
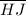 is (2, 2) and the midpoint of
is (2, 2) and the midpoint of
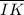 is (2, 2)
is (2, 2)
Therefore, HIJK is a parallelogram because the diagonals have a common midpoint which means they bisect each other