Question

Write the slope-intercept form (y=mx + b) of the blue line. Explain or show your work. Write a one sentence summary comparing the blue line to the black line. Hint: Find the y-intercept. Then count up and over (y/x) to the next point on the line to determine the slope.

Answer 1

Therefore, the slope-intercept form of the blue line is

`y = (1 )/(2)x + 2`

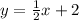
Comparison:

The blue and black lines both have equal y-intercept but different slopes.

The black line is steeper than blue line which means the black line has a greater slope than the blue line.

Explanation:

Please refer to the attached graph of this question where we have two straight lines.

The slope-intercept form is given by

`y = mx + b`

Where m is the slope of the line and b is the y-intercept.

Let us find the slope of the blue line from the points given in the graph.

`(x_1, y_1) = (0,2) \\\\(x_2, y_2) = (4,4) \\\\`

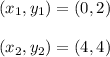
The slope is given by

`m = (y_2 -y_1 )/(x_2 -x_1) \\\\m = (4 -2 )/(4 -0) \\\\m = (2 )/(4) \\\\m = (1 )/(2) \\\\`

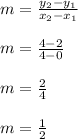
The y-intercept is given by

`y = (1 )/(2)x + b \\\\2 = (1 )/(2)(0) + b \\\\b = 2`

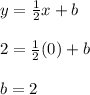
Therefore, the slope-intercept form of the blue line is

`y = (1 )/(2)x + 2`

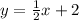
Comparison:

The blue and black lines both have equal y-intercept but different slopes.

The black line is steeper than blue line which means the black line has a greater slope than the blue line.