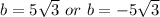Question

Which are the roots of the quadratic function f(b) = 62 – 75? Select two options.

b=573

Ob= -573

b=35

b= -35

Ob= 253

Answer 1

`b = 5 √(3) \ or\ b = -5 √(3)`

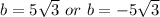
Explanation:

Given

`f(b) = b^2 - 75`

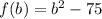
Required

Determine the roots

To get the root of the function, then f(b) must be 0;

i.e. f(b) = 0

So, the expression becomes

`0 = b^2 - 75`

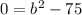
Add 75 to both sides

`75 + 0 = b^2 - 75 + 75`

`75 = b^2`

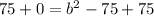
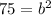
Take square roots of both sides

`√(75) = √(b^2)`

`√(75) = b`

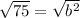
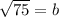
Reorder

`b = √(75)`

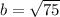
Expand 75 as a product of 25 and 3

`b = √(25*3)`

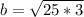
Split the expression

`b = √(25) *√(3)`

`b = \±5 *√(3)`

`b = \±5 √(3)`

`b = 5 √(3) \ or\ b = -5 √(3)`

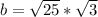
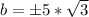
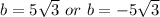
The options are not clear enough; however the roots of the equation are
`b = 5 √(3) \ or\ b = -5 √(3)`