Choice A:
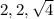
Choice B: 9, 40, 41
Choice C:
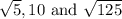
Answer:
(B)9, 40, 41
Explanation:
To check if the sides form a right triangle, you check to see if they satisfy the Pythagorean theorem.
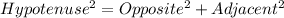
Note that the longest side length is always the hypotenuse.
Choice A:
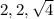
Now,
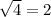
Therefore:
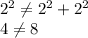
These side lengths form an equilateral triangle. They do not satisfy the theorem.
Choice B: 9, 40, 41
The longest side length is 41.
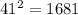
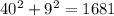
Therefore:
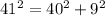
These side lengths form a right triangle.
Choice C:
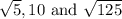
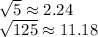
Therefore, the longest side length is
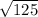
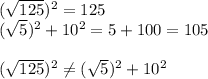
These side lengths do not form a right triangle.