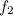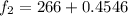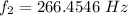Answer:
The lower frequency is
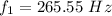
The higher frequency is
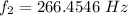
Step-by-step explanation:
From the question we are told that
The period is
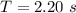
The frequency of the tuning fork is
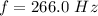
Generally the beat frequency is mathematically represented as
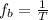
substituting values
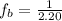
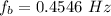
Since the beat frequency is gotten from the beat produced by the tuning fork and and the string then
The possible frequency of the string ranges from
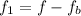
to
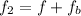
Now substituting values
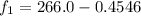
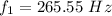
For