Question

ABCD is a square. The length of each side of the square ABCD is units, and the length of its diagonal is about units.

Answer 1

19.8

Explanation:

As per the diagram the solution of the length of side AB, we will use Pythagoras theorem on the right triangle. The base of the AB is the two right triangles.

Now, the first right triangle with a hypotenuse which is 13 and height which is 12, and we will assume x be the base, Now, we will use the hypotenuse: -

`13^2 = 12^2 + x^2\\\\169 = 144 + x^2\\\\x^2 = 169 - 144\\\\x^2 = 25x = √(25)`

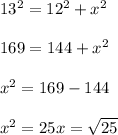
= 5

Now, for the second right triangle with a hypotenuse which is 15 and height which is 12, and we will assume y be the base, so we will use the hypotenuse:-

`15^2 = 12^2 + x^2\\\\225 = 144 + x^2\\\\x^2 = 225 - 144\\\\x^2 = 81x\\\\= √(81)`

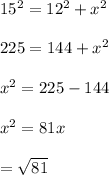
= 9

After solving x and y we will get the length of AB which is

= x + y

= 9 + 5

= 14 unit

So, for a square, all the sides are the same, so the length of each side of the square ABCD

14 units

Now, In triangle ADC, the hypotenuse = AC, AD = DC = 14 unit.

Using Pythagoras:

`AC^2 = AD^2 + DC^2\\\\AC^2 = 14^2 + 14^2AC^2 = 196 + 196 \\\\= 392\\\\AC = √(392)`

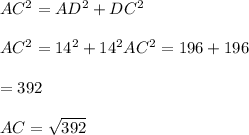
= 19.8