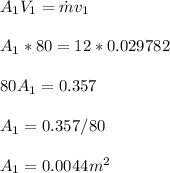Answer:
a) The change in Kinetic energy, KE = -1.95 kJ
b) Power output, W = 10221.72 kW
c) Turbine inlet area,
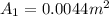
Step-by-step explanation:
a) Change in Kinetic Energy
For an adiabatic steady state flow of steam:
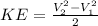 .........(1)
.........(1)
Where Inlet velocity, V₁ = 80 m/s
Outlet velocity, V₂ = 50 m/s
Substitute these values into equation (1)
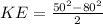
KE = -1950 m²/s²
To convert this to kJ/kg, divide by 1000
KE = -1950/1000
KE = -1.95 kJ/kg
b) The power output, w
The equation below is used to represent a steady state flow.
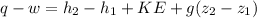
For an adiabatic process, the rate of heat transfer, q = 0
z₂ = z₁
The equation thus reduces to :
w = h₁ - h₂ - KE...........(2)
Where Power output,
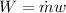 ..........(3)
..........(3)
Mass flow rate,
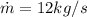
To get the specific enthalpy at the inlet, h₁
At P₁ = 10 MPa, T₁ = 450°C,
h₁ = 3242.4 kJ/kg,
Specific volume, v₁ = 0.029782 m³/kg
At P₂ = 10 kPa,
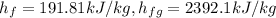 , x₂ = 0.92
, x₂ = 0.92
specific enthalpy at the outlet, h₂ =
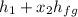
h₂ = 3242.4 + 0.92(2392.1)
h₂ = 2392.54 kJ/kg
Substitute these values into equation (2)
w = 3242.4 - 2392.54 - (-1.95)
w = 851.81 kJ/kg
To get the power output, put the value of w into equation (3)
W = 12 * 851.81
W = 10221.72 kW
c) The turbine inlet area