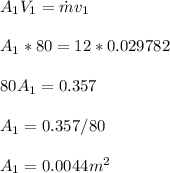Question

Steam flows steadily through an adiabatic turbine. The inlet conditions of the steam are 10 MPa, 450°C, and 80 m/s, and the exit conditions are 10 kPa, 92% quality, and 50 m/s. The mass flow rate of the steam is 12 kg/s.

Determine:
(a) the change in kinetic energy
(b) the power output
(c) the turbine inlet area

Answer 1

a) The change in Kinetic energy, KE = -1.95 kJ

b) Power output, W = 10221.72 kW

c) Turbine inlet area,
`A_1 = 0.0044 m^2`

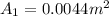
Step-by-step explanation:

a) Change in Kinetic Energy

For an adiabatic steady state flow of steam:

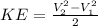`KE = (V_2^2 - V_1^2)/(2) \\`.........(1)

Where Inlet velocity, V₁ = 80 m/s

Outlet velocity, V₂ = 50 m/s

Substitute these values into equation (1)

`KE = (50^2 - 80^2)/(2) \\`

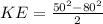
KE = -1950 m²/s²

To convert this to kJ/kg, divide by 1000

KE = -1950/1000

KE = -1.95 kJ/kg

b) The power output, w

The equation below is used to represent a steady state flow.

`q - w = h_2 - h_1 + KE + g(z_2 - z_1)`

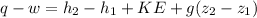
For an adiabatic process, the rate of heat transfer, q = 0

z₂ = z₁

The equation thus reduces to :

w = h₁ - h₂ - KE...........(2)

Where Power output,
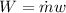`W = \dot{m}w`..........(3)

Mass flow rate,
`\dot{m} = 12 kg/s`

To get the specific enthalpy at the inlet, h₁

At P₁ = 10 MPa, T₁ = 450°C,

h₁ = 3242.4 kJ/kg,

Specific volume, v₁ = 0.029782 m³/kg

At P₂ = 10 kPa,
`h_f = 191.81 kJ/kg, h_(fg) = 2392.1 kJ/kg`, x₂ = 0.92

specific enthalpy at the outlet, h₂ =
`h_1 + x_2 h_(fg)`

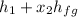
h₂ = 3242.4 + 0.92(2392.1)

h₂ = 2392.54 kJ/kg

Substitute these values into equation (2)

w = 3242.4 - 2392.54 - (-1.95)

w = 851.81 kJ/kg

To get the power output, put the value of w into equation (3)

W = 12 * 851.81

W = 10221.72 kW

c) The turbine inlet area

`A_1V_1 = \dot{m}v_1\\\\A_1 * 80 = 12 * 0.029782\\\\80A_1 = 0.357\\\\A_1 = 0.357/80\\\\A_1 = 0.0044 m^2`