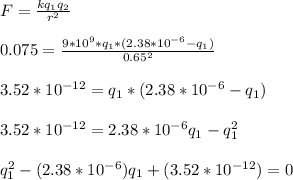Note that the methods applied in solving this question is the appropriate method. Check the parameters you gave in the question if you did not expect a complex number for the charges. Thanks
Answer:

Step-by-step explanation:
Note: When a conducting wire was connected between the spheres, the same charge will flow through the two spheres.
The two charges were 0.65 m apart. i.e. d = 0.65 m
Force, F = 0.030 N
The force or repulsion between the two charges can be calculated using the formula:

Due to the wire connected between the two spheres,
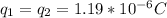
The sum of the charges on the two spheres =
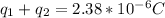
Note: When the conducting wire is removed, the two spheres will no longer contain similar charges but will rather share the total charge unequally
Let charge in the first sphere =
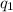
Charge in the second sphere, q₂ =
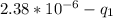
Force, F = 0.075 N