Given:
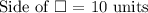
Area of square:
The area of the square can be determined by using the formula "(side)²".
⇒ Area of square = (side)²
⇒ = (10)² [Side = 10 units]
⇒ = (10)(10)
⇒ = 100 units²
Therefore, the area of the square is 100 units².
Perimeter of square:
The perimeter of the square can be found by using the formula "4(side)".
⇒ Perimeter of square = 4(side)
⇒ = 4(10)
⇒ = 4 × 10
⇒ = 40 units
Furthermore, the question says:
Which is greater?
- The number of square units (100) for the area of the square.
- The number of units (40) for the perimeter
Conclusion: Since 100 is greater than 40, the number of square units for the area of the square is greater than the number of units for the perimeter.