Question

One side of a square is 10 units. Which is greater, the number of square units for the area of the square or the number of units for the perimeter? Explain.

Answer 1

Given:

`\text{Side of }\square \ \text{= 10 units}`

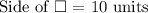
Area of square:

The area of the square can be determined by using the formula "(side)²".

⇒ Area of square = (side)²

⇒ = (10)² [Side = 10 units]

⇒ = (10)(10)

⇒ = 100 units²

Therefore, the area of the square is 100 units².

Perimeter of square:

The perimeter of the square can be found by using the formula "4(side)".

⇒ Perimeter of square = 4(side)

⇒ = 4(10)

⇒ = 4 × 10

⇒ = 40 units

Furthermore, the question says:

Which is greater?

- The number of square units (100) for the area of the square.

- The number of units (40) for the perimeter

Conclusion: Since 100 is greater than 40, the number of square units for the area of the square is greater than the number of units for the perimeter.