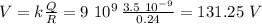Answer:
(a) V = 65.625 Volts
(b) V = 131.25 Volts
(c) V = 131.25 Volts
Step-by-step explanation:
Recall that:
1) in a metal sphere the charges distribute uniformly around the surface, and the electric field inside the sphere is zero, and the potential is constant equal to:
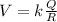
2) the electric potential outside of a charged metal sphere is the same as that of a charge of the same value located at the sphere's center:
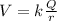
where k is the Coulomb constant (
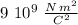 ), Q is the total charge of the sphere, R is the sphere's radius (0.24 m), and r is the distance at which the potential is calculated measured from the sphere's center.
), Q is the total charge of the sphere, R is the sphere's radius (0.24 m), and r is the distance at which the potential is calculated measured from the sphere's center.
Then, at a distance of:
(a) 48 cm = 0.48 m, the electric potential is:
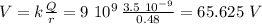
(b) 24 cm = 0.24 m, - notice we are exactly at the sphere's surface - the electric potential is:
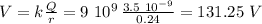
(c) 12 cm (notice we are inside the sphere, and therefore the potential is constant and the same as we calculated for the sphere's surface: