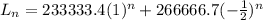Answer: a. Ln =
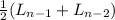
b.
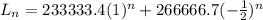
Explanation: Recurrence Relation is a polynomial that relates a term in a sequence with its previous terms.
a. The number of lobster is the average of two previous years. Average is the sum of the elements of a set divided by the total number of the set, so for Ln:
Ln =
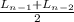 =
=
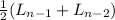
where
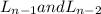 are the two previous years.
are the two previous years.
b) Ln =
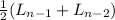
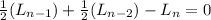
To solve this recurrence, find the characteristic polynomial:
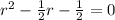
Solve for r:
The polynomial can be rewritten as:
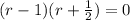
so, r = 1 and r = -1/2
The expression for the recurrence relation will be:
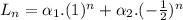
In year 1, there were 100,000 lobsters, so, when n=1:
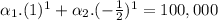
In year 2, when n=2, Ln = 300,000:
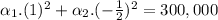
Solving the system of equations:
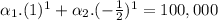
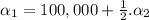
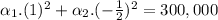
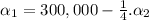
Finding
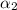 :
:
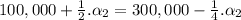
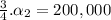
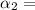 266666.7
266666.7
With
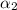 , plug in an equation to find
, plug in an equation to find
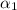 :
:
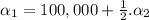
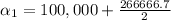
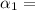 233333.4
233333.4
The solved equation for this recurrence relation is: