Question

A model for the number of lobsters caught per year is based on the assumption that the number of lobsters caught in a year is the average of the number caught in two previous years. (Show your work, circle or put in bold each intermediate and final answer.)

a. Find a recurrence relation for Ln -- the number of lobsters caught in year n.
b. Solve this recurrence relation (find Ln), if 100,000 lobsters were caught in year 1 and 300,000 lobsters were caught in year 2.

Answer 1

Answer: a. Ln =
`(1)/(2) (L_(n-1) + L_(n-2))`

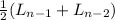
b.
`L_(n) = 233333.4(1)^(n)+266666.7(-(1)/(2) )^(n)`

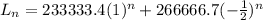
Explanation: Recurrence Relation is a polynomial that relates a term in a sequence with its previous terms.

a. The number of lobster is the average of two previous years. Average is the sum of the elements of a set divided by the total number of the set, so for Ln:

Ln =
`(L_(n-1)+L_(n-2))/(2)` =
`(1)/(2)(L_(n-1)+L_(n-2))`

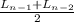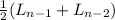
where
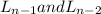`L_(n-1) and L_(n-2)` are the two previous years.

b) Ln =
`(1)/(2)(L_(n-1)+L_(n-2))`

`(1)/(2)(L_(n-1))+(1)/(2) (L_(n-2)) - L_(n) = 0`

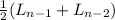
To solve this recurrence, find the characteristic polynomial:

`r^(2) - (1)/(2)r - (1)/(2) = 0`

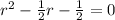
Solve for r:

The polynomial can be rewritten as:

`(r-1)(r+(1)/(2) )=0`

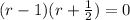
so, r = 1 and r = -1/2

The expression for the recurrence relation will be:

`L_(n) = \alpha_(1) .(1)^(n) + \alpha_(2).(-(1)/(2) )^(n)`

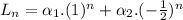
In year 1, there were 100,000 lobsters, so, when n=1:

`\alpha_(1) .(1)^(1) + \alpha_(2).(-(1)/(2) )^(1) = 100,000`

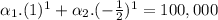
In year 2, when n=2, Ln = 300,000:

`\alpha_(1) .(1)^(2) + \alpha_(2).(-(1)/(2) )^(2) = 300,000`

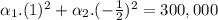
Solving the system of equations:

`\alpha_(1) .(1)^(1) + \alpha_(2).(-(1)/(2) )^(1) = 100,000`

`\alpha_(1) = 100,000 + (1)/(2).\alpha_(2)`

`\alpha_(1) .(1)^(2) + \alpha_(2).(-(1)/(2) )^(2) = 300,000`

`\alpha_(1) = 300,000 - (1)/(4).\alpha_(2)`

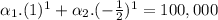
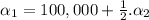
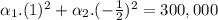
Finding
`\alpha _(2)`:

`100,000+(1)/(2).\alpha_(2) = 300,000 - (1)/(4).\alpha_(2)`

`(3)/(4).\alpha_(2) = 200,000`

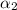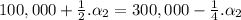
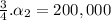
`\alpha_(2) =` 266666.7

With
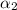`\alpha _(2)`, plug in an equation to find
`\alpha_(1)`:

`\alpha_(1) = 100,000 + (1)/(2).\alpha_(2)`

`\alpha_(1) = 100,000 + (266666.7)/(2)`

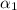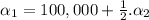
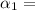`\alpha_(1) =` 233333.4

The solved equation for this recurrence relation is:

`L_(n) = 233333.4(1)^(n) + 266666.7(-(1)/(2))^(n)`