Question

A thermal energy storage unit consists of a large rectangular channel, which is well insulated on its outer surface and encloses alternating layers of the storage material and the flow passage. Each layer of the storage material is an aluminum slab of width W=0.05 m, which is at an initial temperature of 25∘C25 ∘C. Consider conditions for which the storage unit is charged by passing a hot gas through the passages, with the gas temperature and the convection coefficient assumed to have constant values of T[infinity]=600∘CT [infinity]=600 ∘C and h=100W/m2⋅Kh=100W/m 2⋅K throughout the channel. How long will it take to achieve 75% of the maximum possible energy storage? What is the temperature of the aluminum at this time?

Answer 1

the temperature of the aluminum at this time is 456.25° C

Step-by-step explanation:

Given that:

width w of the aluminium slab = 0.05 m

the initial temperature
`T_1` = 25° C

`T{\infty} =600^0C`

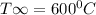
h = 100 W/m²

The properties of Aluminium at temperature of 600° C by considering the conditions for which the storage unit is charged; we have ;

density ρ = 2702 kg/m³

thermal conductivity k = 231 W/m.K

Specific heat c = 1033 J/Kg.K

Let's first find the Biot Number Bi which can be expressed by the equation:

`Bi = (hL_c)/(k) \\ \\ Bi = (h (w)/(2))/(k)`

`Bi = (hL_c)/(k) \\ \\ Bi = (100 * (0.05)/(2))/(231)`

`Bi = (2.5)/(231)`

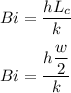
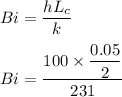
Bi = 0.0108

The time constant value
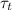`\tau_t` is :

`\tau_t = (pL_cc)/(h) \\ \\ \tau_t = (p (w)/(2)c)/(h)`

`\tau_t = (2702* (0.05)/(2)*1033)/(100)`

`\tau_t = (2702* 0.025*1033)/(100)`

`\tau_t = 697.79`

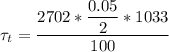
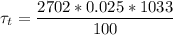
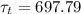
Considering Lumped capacitance analysis since value for Bi is less than 1

Then;

`Q= (pVc)\theta_1 [1-e^{\frac {-t}{ \tau_1}}]`

where;

`Q = -\Delta E _(st)` which correlates with the change in the internal energy of the solid.

So;

`Q= (pVc)\theta_1 [1-e^{\frac {-t}{ \tau_1}}]= -\Delta E _(st)`

The maximum value for the change in the internal energy of the solid is :

`(pVc)\theta_1 = -\Delta E _(st)max`

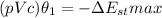
By equating the two previous equation together ; we have:

`\frac{-\Delta E _(st)}{\Delta E _(st){max}}= \frac{ (pVc)\theta_1 [1-e^{\frac {-t}{ \tau_1}}]} { (pVc)\theta_1}`

Similarly; we need to understand that the ratio of the energy storage to the maximum possible energy storage = 0.75

Thus;

`0.75= [1-e^{\frac {-t}{ \tau_1}}]}`

So;

`0.75= [1-e^{\frac {-t}{ 697.79}}]}`

`1-0.75= [e^{\frac {-t}{ 697.79}}]}`

`0.25 = e^{\frac {-t}{ 697.79}}`

`In(0.25) = {\frac {-t}{ 697.79}}`

`-1.386294361= (-t)/(697.79)`

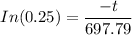
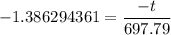
t = 1.386294361 × 697.79

t = 967.34 s

Finally; the temperature of Aluminium is determined as follows;

`(T - T _(\infty))/(T_1-T_(\infty))= e ^ {(-t)/(\tau_t)}`

`(T - 600)/(25-600)= e ^ {(-967.34)/(697.79)`

`(T - 600)/(25-600)= 0.25`

`(T - 600)/(-575)= 0.25`

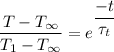
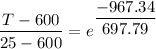
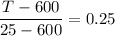
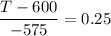
T - 600 = -575 × 0.25

T - 600 = -143.75

T = -143.75 + 600

T = 456.25° C

Hence; the temperature of the aluminum at this time is 456.25° C