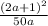Answer:
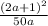
Explanation:
Given
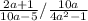
Required
Find the equivalent
We start by changing the / to *
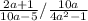
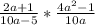
Factorize 10a - 5
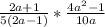
Expand 4a² - 1
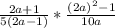
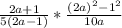
Express (2a)² - 1² as a difference of two squares
Difference of two squares is such that:
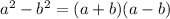
The expression becomes
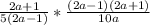
Combine both fractions to form a single fraction
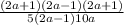
Divide the numerator and denominator by 2a - 1
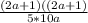
Simplify the numerator
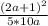
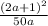
Hence,
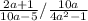 =
=