Question

An automobile travels along a straight road at 15.65 m/s through a 11.18 m/s speed zone. A police car observed the automobile. At the instant that the two vehicles are abreast of each other, the police car starts to pursue the automobile at a constant acceleration of 1.96 m/s2 . The motorist noticed the police car in his rear view mirror 12 s after the police car started the pursuit and applied his brakes and decelerates at 3.05 m/s2

Answer 1

An automobile travels along a straight road at 15.65 m/s through a 11.18 m/s speed zone. A police car observed the automobile. At the instant that the two vehicles are abreast of each other, the police car starts to pursue the automobile at a constant acceleration of 1.96 m/s2 . The motorist noticed the police car in his rear view mirror 12 s after the police car started the pursuit and applied his brakes and decelerates at 3.05 m/s2

Find the total time required for the police car to over take the automobile.

Answer:

15.02 sec

Step-by-step explanation:

The total time required for the police car to overtake the automobile is related to the distance covered by both cars which is equal from instant point of abreast.

So; we can say :

`D_(pursuit) =D_(police)`

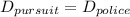
By using the second equation of motion to find the distance S;

`S= ut + (1)/(2)at^2`

`D_(pursuit) = (15.65 *12 )+(15.65 (t)+ ((1)/(2)*(-3.05)t^2)`

`D_(pursuit) = (187.8)+(15.65 \ t)-0.5*(3.05)t^2)`

`D_(pursuit) = (187.8+15.65 \ t-1.525 t^2)`

`D_(police) = ut _P + (1)/(2)at_p^2`

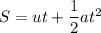
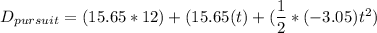
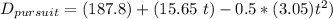
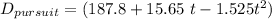
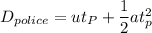
where ;

u = 0

`D_(police) = (1)/(2)at_p^2`

`D_(police) = (1)/(2)*(1.96)*(t+12)^2`

`D_(police) = 0.98*(t+12)^2`

`D_(police) = 0.98*(t^2 + 144 + 24t)`

`D_(police) = 0.98t^2 + 141.12 + 23.52t`

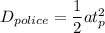
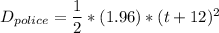
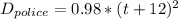
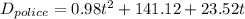
Recall that:

`D_(pursuit) =D_(police)`

`(187.8+15.65 \ t-1.525 t^2)= 0.98t^2 + 141.12 + 23.52t`

`(187.8 - 141.12) + (15.65 \ t - 23.52t) -( 1.525 t^2 - 0.98t^2) = 0`

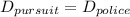
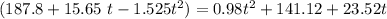
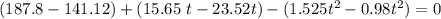
= 46.68 - 7.85 t -2.505 t² = 0

Solving by using quadratic equation;

t = -6.16 OR t = 3.02

Since we can only take consideration of the value with a positive integer only; then t = 3.02 secs

From the question; The motorist noticed the police car in his rear view mirror 12 s after the police car started the pursuit;

Therefore ; the total time required for the police car to over take the automobile = 12 s + 3.02 s

Total time required for the police car to over take the automobile = 15.02 sec