Question

8. A model airplane is shot into the air. Its path is approximated by the

function h (t) = -5r2 + 251, where h(t) is the height in metres and
is the time in seconds. When will the airplane hit the ground?

Answer 1

Here is another one of those " quadratic word problems " at hand, which is great!

By the function that is given to us ( which I believe is meant to be
`h(t) = - 5t^2 + 251` ) the airplane is launched at a height of 251 metres, with no velocity. Anyhow, we need to determine the duration with which the airplane will strike the ground, and to do so we can set up the following equation,
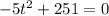`- 5t^2 + 251 = 0` - solving for t, otherwise known to be the time!

See the procedure below -

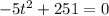`-5t^2+251=0` - Subtract 251 from either side,

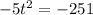`-5t^2=-251` - Divide either side by - 5,

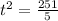`t^2=(251)/(5)` - And, now isolate t, receiving two solutions,

`t=\sqrt{(251)/(5)},\:t=-\sqrt{(251)/(5)}`

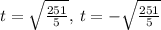
However, time can't be a negative value. Thus our solution is
`√(251 / 5)`, which is ( about ) 7.085 seconds!