Answer:
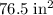 .
.
Explanation:
The triangular prism shown in the diagram has five faces:
- Two (identical) triangular faces at the top and bottom of this prism, and
- Three rectangles for the faces on the side.
Triangular faces
Note that the two triangular faces at the top and bottom are identical. (In other words, these two triangles are congruent, with the same shape and area.)
From the numbers near the triangle at the top of this prism, each of the two triangles has a height of
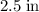 on a base of length
on a base of length
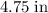 . The area of each of these triangles would be:
. The area of each of these triangles would be:
 .
.
There are two such triangular faces in this prism. When combined, these two faces will contribute an area of
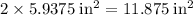 to the surface area of this prism.
to the surface area of this prism.
Rectangular faces
There are three rectangular faces on the sides of this triangular prism. They have different lengths but share the same width:
- The lengths of the three rectangular faces are
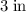 ,
,
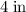 , and
, and
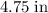 . (Note that the
. (Note that the - The heights of these three rectangular faces are all equal to
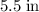 .
.
The area of these three rectangles, combined. will be:
 .
.
Total surface area of the prism
Combine the surface area of the five faces to obtain the surface area of this triangular prism:
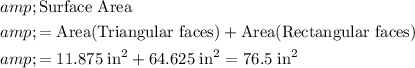 .
.