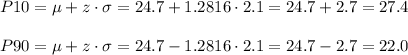Answer:
P10 = 27.4
P90 = 22.0
It helps the producer to know the higher (P10) and lower estimates (P90) for the amount of chocolate chips per cookie.
Explanation:
In P10 and P90 the P stands for "percentile".
In the case of P10, indicates the value X of the random variable for which 10% of the observed values will be above this value X.
In the case of P90, this percentage is 90%.
In this case, we can calculate from the z-values for each of the percentiles in the standard normal distribution.
For P10 we have:
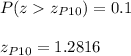
For P90 we have:
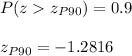
Then, we can convert this values to our normal distribution as: