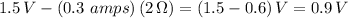Question

PLEASE HELP ME ASAP

1.A resistor of 3 ohms is connected to a battery of Emf 6V .If the internal resistance of the battery is 2A. calculate the current flowing in the circuit and draw the circuit diagram.
2. A cell of Emf 1.5V with internal resistance of 2 ohms is connected to two 6 ohms resistors in parallel.
Calculate:
a. The combined Resistance of the 6ohms resistors in parallel.
b. The current supplied by the cell
c. The potential difference across the terminals.
​

Answer 1

1. Current in the circuit; 1.2 Amps

See attached image for the circuit.

2. Equivalent resistor = 3 Ω

I = 0.3 amps

Potential difference across the battery terminals is: 0.9 V

Step-by-step explanation:

Part 1.

The internal resistance of 2 ohms is simply added to the circuit in series as shown in the attached image.

Since now we have two resistances in series (2 ohms and 3 ohms) the total of this series combination is 5 ohms. Using Ohm's law, we can derive the current running through the circuit:

`V=I\,\,R\\6\,V=I\,(5\,\Omega)\\I=(6)/(5) \,amps\\I=1.2\,\,amps`

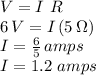
Part 2.

Now we have a 1.5 V battery with a 2 ohm internal resistance, connected to two identical 6 ohm resistors.

a. The equivalent resistance presented by the two resistors in parallel:

`(i)/(R_e) =(1)/(6\,\Omega) + (1)/(6\,\Omega) =(1)/(3\,\Omega) \\R_e=3\,\Omega`

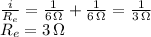
b. Now the circuit can be represented by a 2 ohm resistor (internal battery resistance) plus a 3 ohm parallel equivalent resistor in series. That is a 5 ohm total resistance. Then Ohm's law becomes:

`V=I\,\,R\\1.5\,V=I\,(5\,\Omega)\\I=(1.5)/(5) \,amps\\I=0.3\,\,amps`

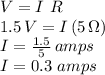
c. The potential difference across the battery terminals must be the battery's EMF minus the potential drop in its internal resistance:

`1.5\,V - (0.3\,\,amps)\,(2\,\Omega)=(1.5-0.6)\,V=0.9\,V`