Question

Consider the functions f(x) = 3x?, g(x) = g, and h(x) = 3x.

Which statements accurately compare the domain and range of the functions? Select two options.

All of the functions have a unique range.

The range of all three functions is all real numbers.

The domain of all three functions is all real numbers.

The range of f(x) and h(x) is all real numbers, but the range of g(x) is all real numbers except 0.

The domain of f(x) and h(x) is all real numbers, but the domain of g(x) is all real numbers except 0.

Answer 1

(D)The range of f(x) and h(x) is all real numbers, but the range of g(x) is all real numbers except 0.

(E)The domain of f(x) and h(x) is all real numbers, but the domain of g(x) is all real numbers except 0.

Explanation:

2021 EDGE

Answer 2

Question Correction

The functions are
`f(x) = 3x^2, g(x)=(1)/(3x),$ and h(x) = 3x.`

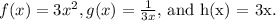
Answer:

(D)The range of f(x) and h(x) is all real numbers, but the range of g(x) is all real numbers except 0.

(E)The domain of f(x) and h(x) is all real numbers, but the domain of g(x) is all real numbers except 0.

Explanation:

Definition: Given a function f(x):

• The domain of f(x) are the values of x at which f(x) is defined.
• The range of the function are the values of f(x) which is defined.

In g(x), there is no value of x that will make g(x)=0. Therefore, the range of f(x) and h(x) is all real numbers, but the range of g(x) is all real numbers except 0.

In g(x), when x=0

`g(x)=(1)/(3(0))=(1)/(0)`

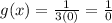
Therefore,g(x) is undefined at x=0.

However, at x=0, f(x)=0 and h(x)=0 which are defined.

Therefore, the domain of f(x) and h(x) is all real numbers, but the domain of g(x) is all real numbers except 0.