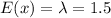Question

The number of people arriving for treatment at an emergency room can be modeled by a Poisson process with a rate parameter of six per hour.

(a) What is the probability that exactly three arrivals occur during a particular hour? (Round your answer to three decimal places.)
(b) What Is the probability that at least three people arrive during a particular hour? (Round your answer to three decimal places.)
(c) How many people do you expect to arrive during a 15-min period?

Answer 1

a) P(x=3)=0.089

b) P(x≥3)=0.938

c) 1.5 arrivals

Explanation:

Let t be the time (in hours), then random variable X is the number of people arriving for treatment at an emergency room.

The variable X is modeled by a Poisson process with a rate parameter of λ=6.

The probability of exactly k arrivals in a particular hour can be written as:

`P(x=k)=\lambda^(k) \cdot e^(-\lambda)/k!\\\\P(x=k)=6^k\cdot e^(-6)/k!`

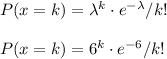
a) The probability that exactly 3 arrivals occur during a particular hour is:

`P(x=3)=6^(3) \cdot e^(-6)/3!=216*0.0025/6=0.089\\\\`

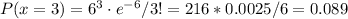
b) The probability that at least 3 people arrive during a particular hour is:

`P(x\geq3)=1-[P(x=0)+P(x=1)+P(x=2)]\\\\\\P(0)=6^(0) \cdot e^(-6)/0!=1*0.0025/1=0.002\\\\P(1)=6^(1) \cdot e^(-6)/1!=6*0.0025/1=0.015\\\\P(2)=6^(2) \cdot e^(-6)/2!=36*0.0025/2=0.045\\\\\\P(x\geq3)=1-[0.002+0.015+0.045]=1-0.062=0.938`

c) In this case, t=0.25, so we recalculate the parameter as:

`\lambda =r\cdot t=6\;h^(-1)\cdot 0.25 h=1.5`

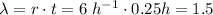
The expected value for a Poisson distribution is equal to its parameter λ, so in this case we expect 1.5 arrivals in a period of 15 minutes.

`E(x)=\lambda=1.5`