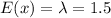Answer:
a) P(x=3)=0.089
b) P(x≥3)=0.938
c) 1.5 arrivals
Explanation:
Let t be the time (in hours), then random variable X is the number of people arriving for treatment at an emergency room.
The variable X is modeled by a Poisson process with a rate parameter of λ=6.
The probability of exactly k arrivals in a particular hour can be written as:
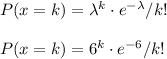
a) The probability that exactly 3 arrivals occur during a particular hour is:
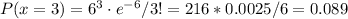
b) The probability that at least 3 people arrive during a particular hour is:
![P(x\geq3)=1-[P(x=0)+P(x=1)+P(x=2)]\\\\\\P(0)=6^(0) \cdot e^(-6)/0!=1*0.0025/1=0.002\\\\P(1)=6^(1) \cdot e^(-6)/1!=6*0.0025/1=0.015\\\\P(2)=6^(2) \cdot e^(-6)/2!=36*0.0025/2=0.045\\\\\\P(x\geq3)=1-[0.002+0.015+0.045]=1-0.062=0.938](https://img.qammunity.org/2021/formulas/mathematics/college/jarrzo9m7khf6saphkx2i72nlxjihmyjse.png)
c) In this case, t=0.25, so we recalculate the parameter as:
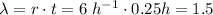
The expected value for a Poisson distribution is equal to its parameter λ, so in this case we expect 1.5 arrivals in a period of 15 minutes.