Answer:
(a)Charlie is right
(b)$0
Explanation:
(a)A game is said to be a fair game when the probability of winning is equal to the probability of losing. Mathematically, a game is said to be fair when the expected value is zero.
In the game, the possible outcomes are: HH, HT, TH and TT.
Charlie wins when the outcome is HH, TT
- P(Charlie Wins)=2/4
- P(Charlie Losses)=2/4
Lucy wins when the outcome is HT or TH
- P(Lucy Wins)=2/4
- P(Lucy Losses)=2/4
Therefore, the game is fair. Charlie is right.
(b)
If the outcome is HH, Lucy pays $3.
If the outcome is HT or TH, Lucy gets $2.
If the outcome is TT, Lucy pays $1.
The probability distribution of Lucy's profit is given below:
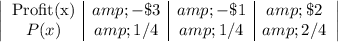
Expected Profit
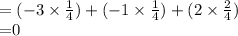
Lucy's expected profit from the game is $0.